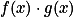实变函数:可测函数

日期: 2016-08-14 标签: [publish]
=== === === ===

设f(x)是定义在可测集 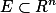$E \subset R^n$ 的实函数，如果
对于任意有限实数a, E[f >a] 都是可测集，则称f(x)定义在E
上的可测函数.

定理
设f(x)是定义在可测集E上的实函数，下列任一条件都是f(x)在E上可测的充要条件:
1,对任何有限实数a, $E[f \ge a]$ 都可测
2,对任何有限实数a, E [f <a] 都可测。
3,对任何有限实数a, $E[f \le a ]$ 都可测。

定理
可测集 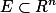$E \subset R^n$ 上的连续函数都是可测函数。

定理
(1) 设f(x)是可测集E上可测函数，而 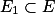$E_1 \subset E$ 为E的可测子集，
则f(x)是看作定义在 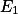E_1 上的函数时，它是 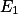E_1 上
的可测函数
(2) 设f(x)是定义在有限个可测集 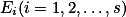$E_i (i=1,2,\dots,s)$ 的并集
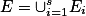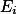$E= \cup_{i=1}^s E_i$ 上，且f(x)在每个 E_i 上可测，则f(x) 在E上也可测。

引理
设 f(x) 与 g(x)为有上可测函数，则 E[f >g] 与 $E[f \ge t]$ 都是可测集。

设f(x),g(x)在E上可测，则下列函数（假定它们在E上有意义)皆在E上可测：
(1) f(x)+g(x)
(2) |f(x)|
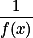
(3) $\frac 1 {f(x)}$
(4) $f(x) \cdot g(x)$